January 4, 2021

Guqin Part 2: Open and Pressed Notes

In the last part of this series, Guqin Part 1: Harmonics and Hui Positions, I look at how harmonics determine the position of the 13 Huis (Huī 徽). These are the dots at the top of the Guqin, pictured below.

Here's a representation of the Hui marks underneath a treble clef staff (clef not shown.. obviously).

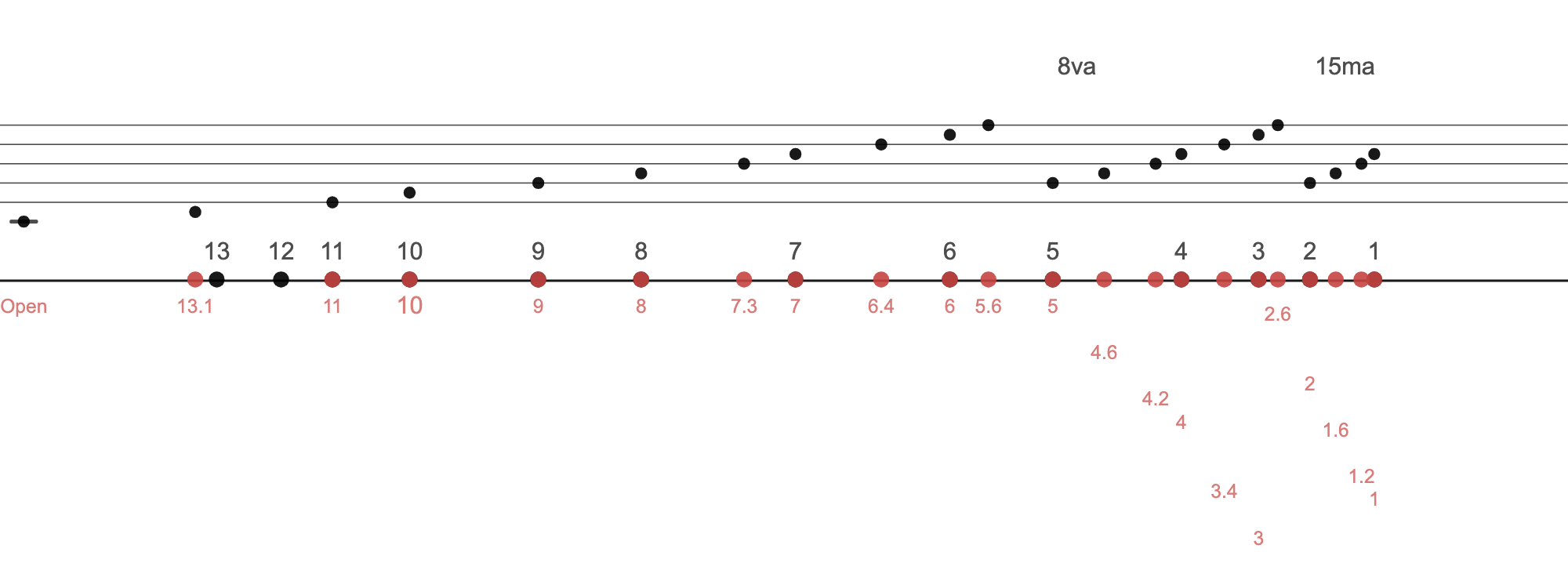
These 13 Huis are the only helpers for figuring out where to press down for the pressed notes (or Àn Yīn 按音). In Guqin notation, instructions would say something like "place left ring finger on 9.5 hui," but is 9.5 Hui actually the right position for that note, or is it 9.6? Or something in between?

1: Playing Octaves

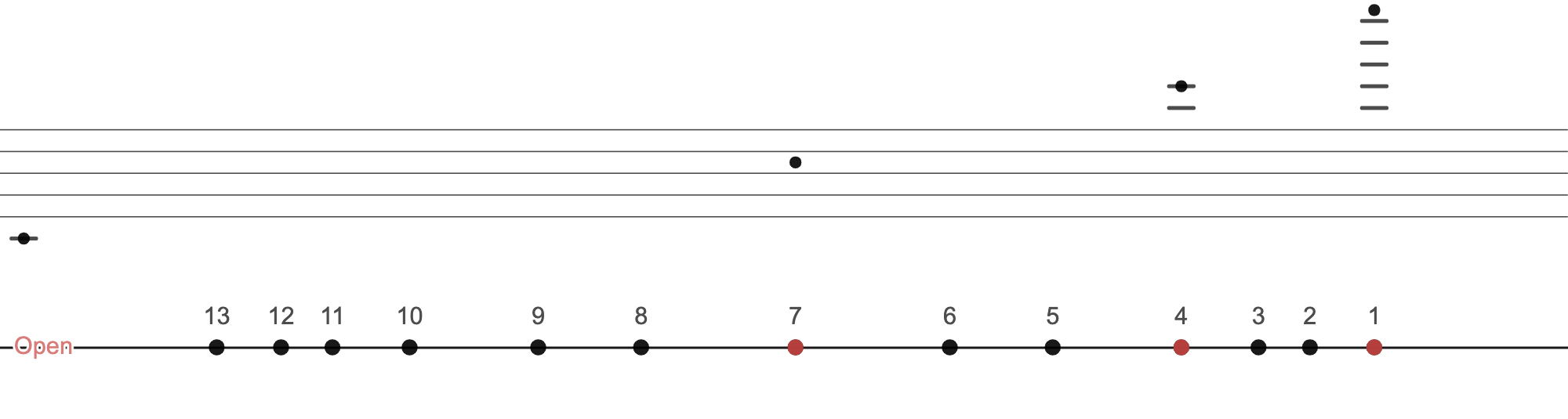
Now, it just so happens that music follows a mathematical formula to dictate where we should press down on a string in order to play which note. Essentially, if we half the string, we raise one octave above the open string (Sàn Yīn 散音) pitch, we half that, we raise another octave.

So in the illustration below, if we pluck the open string (left hand takes a break), we get the middle C. If we pluck while the left hand holds the string down half way (at 7th Hui), we get C one octave up. If the left hand presses the string 75% of the way (at 4th Hui), we get C two octaves up.

2: The Intonation Rabbit Hole

Now, imagine there are 1200 little steps in each octaves. These steps are called cents. So middle C = 0 cent; C one octave up = 1200 cents; C two octaves up = 2400 cents; and so on. Depending on what tuning systems is used, each note will have a slightly different cent value. For example, an E has 400 cents using the equal temperament tuning, 407.8 cents using Pythagorean tuning, and 386.3 using the Just tuning.

I am a bit torn on which tuning system to use.

Option 1: The Just Tuning: (Pro) The Just tuning matches the harmonics better, and thus they align more neatly to the hui positioning. (Pro) It also has rounder numbers, so we are less likely to have to press down on something like 10.9 hui to create a note. This is because the positioning of the Huis are done relative to the harmonics, and the Just Intonation is based on harmonics as well. (Con) However, the same notes between different strings will be slightly out of tune, and there are slight differences between flats and sharps, which is bizarre to me as a piano player.
Option 2: The Equal Temperament. The Equal Temperament splits up chromatic notes into 12 even chunks within the 1200 cents octave. So if C has 0 cents, then C#/Db has 100 cents, D has 200 cents, etc. (Pro) This means that A# = Bb, which simplifies the number of notes in the scale. (Pro) It also means the
Option 3 and beyond: Pythagorean Temperament, probably others: There are other intonation systems that I did not spend a lot of time on. Point is, there are others out there in the world and graduate students spending way more time than me picking these apart.

For the purpose of this post, I will just compare differences between Just and Equal Temperament, as it relates to figuring out just where to press to get a note. Since intonation answers the question, just what pitch is a given note.

Just Intonation

Here's an example of the first octave if both the C string and the D string were tuned to the Just Intonation. In "1: C," 1 refers to the octave and C to the note name. So "2: C" is one octave higher than "1: C."

Note that for the same position, the note E's cent value (bolded below) are off by 21.5 cents, which is about 20% of a chromatic interval. [Note: in just intonation charts I found online, flats and sharps sometimes have different cent values. Not wanting to make this more complicated than need be, I just averaged the two so notes like A# would equal Bb]

Position	C String Notes	Cents	D String Notes	Cents
open	1: C	0	1: D	203.9
13.5	1: C#/Db	91.2	1: D#/Eb	295.1
13.1	1: D	203.9	1: E	407.8
12.2	1: D#/Eb	295.1	1: F	499
11	1: E	386.3	1: F#/Gb	590.2
10	1: F	498	1: G	701.9
9.5	1: F#/Gb	600	1: G#/Ab	803.9
9	1: G	702	1: A	905.9
8.5	1: G#/Ab	793.15	1: A#/Bb	997.05
8	1: A	884.4	1: B	1088.3
7.7	1: A#/Bb	986.3	2: C	1190.2
7.3	1: B	1088.3	2: C#/Db	1292.2
7	2: C	1200	2: D	1403.9

Equal Temperament

Compare this with equal temperament intonation, in the table below. The1E is the same in the C string as in the D string. However, there is a teensy little misalignments in where we should press relative to the (harmonic based) huis, like the hui position of 10.9 (not quite 11!) for the major third and the 7.9 (not quite 8!) for the major sixths.

Position	String 1: Note	Cents	String 2: Notes	Cents
14.0	1: C	0	1: D	200
13.6	1: C#/Db	100	1: D#/Eb	300
13.1	1: D	200	1: E	400
12.2	1: D#/Eb	300	1: F	500
10.9	1: E	400	1: F#/Gb	600
10.0	1: F	500	1: G	700
9.5	1: F#/Gb	600	1: G#/Ab	800
9.0	1: G	700	1: A	900
8.4	1: G#/Ab	800	1: A#/Bb	1000
7.9	1: A	900	1: B	1100
7.6	1: A#/Bb	1000	2: C	1200
7.3	1: B	1100	2: C#/Db	1300
7.0	2: C	1200	2: D	1400

I've waffled back and forth a bunch on this. Even in the course of writing this post, I've rewritten my recommendation a few times.

And the winner is...

My final recommendation is this: it depends, and given technology enables us to quickly calculate the hui positioning of different intonation, we can use one intonation one day and another the next. We don't really need to decide.

However, I am going to use the Just intonation for now for two main reasons: (1) it gives me rounder hui positions to work with. That is just easier to process when I'm reading or writing music. If it sounds a bit out of tune, I can always move my finger a bit. I find that as I get to know a piece of music, I rely less on what's I see on the paper and more on what I hear from the instrument. So if the notes are not matching up between the strings exactly, I trust my ear to course correct. (2) Having tried out the two intonations, the Just intonation sounds a bit better. The reasons are unclear, but my gut (my ear's gut?) tells me that's the right way to go.

In all practicality, it will not make a huge different at this stage since the differences in the hui positioning between Just and Equal Temp. are usually under 1/8". Six notes have differences >1/8", with the biggest difference (the major sixths) at 1/2". Different situations might also call for different intonations. When playing with a piano, it might be better to use Equal Temp since that's how pianos are tuned.

2: Calculating Hui Positions

Back out of the rabbit hole. So next step once we figure out what intonation to use (which tells us exactly what pitch a note is), we'll need to figure out where to press down on the string. To figure that out, we need some handy exponents. The formula looks something like this. Where "x" is the cents we are targeting, and f(x) gives we what percentage along the string we should press down.

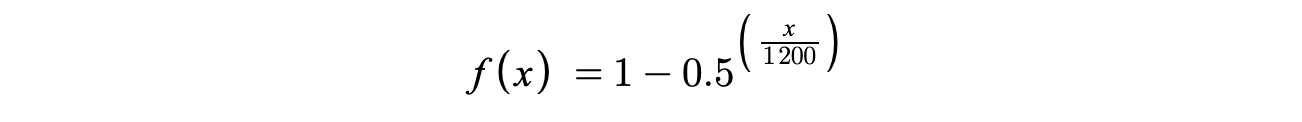
So f(1200) = 0.5, meaning to get a C one octave up, press down on the middle of the string. I tried it. It checks out.

Now that we have (1) positions of where all the Huis are and (2) an understanding of how far along the string (percentage-wise) to press to get our notes, we can get a mapping of the scale relative to the Hui. So 6.5 means press down between 6 Hui and 7 Hui.

3.1: Major Scale

Here's a C major scale. This spans 3 octaves, though I'm not sure if it really makes sense to play beyond the 3rd hui (E three octaves up). For kicks, I'll put in both the C major scale using Just Intonation and Equal Temperament Intonation. There is the slight misalignment I'm talking about with the Equal Temperament intonation, E is not quite on the 11th hui, A is not quite at 8, etc. The red numbers trailing down is just so we can read the hui positions without the numbers running into one another.

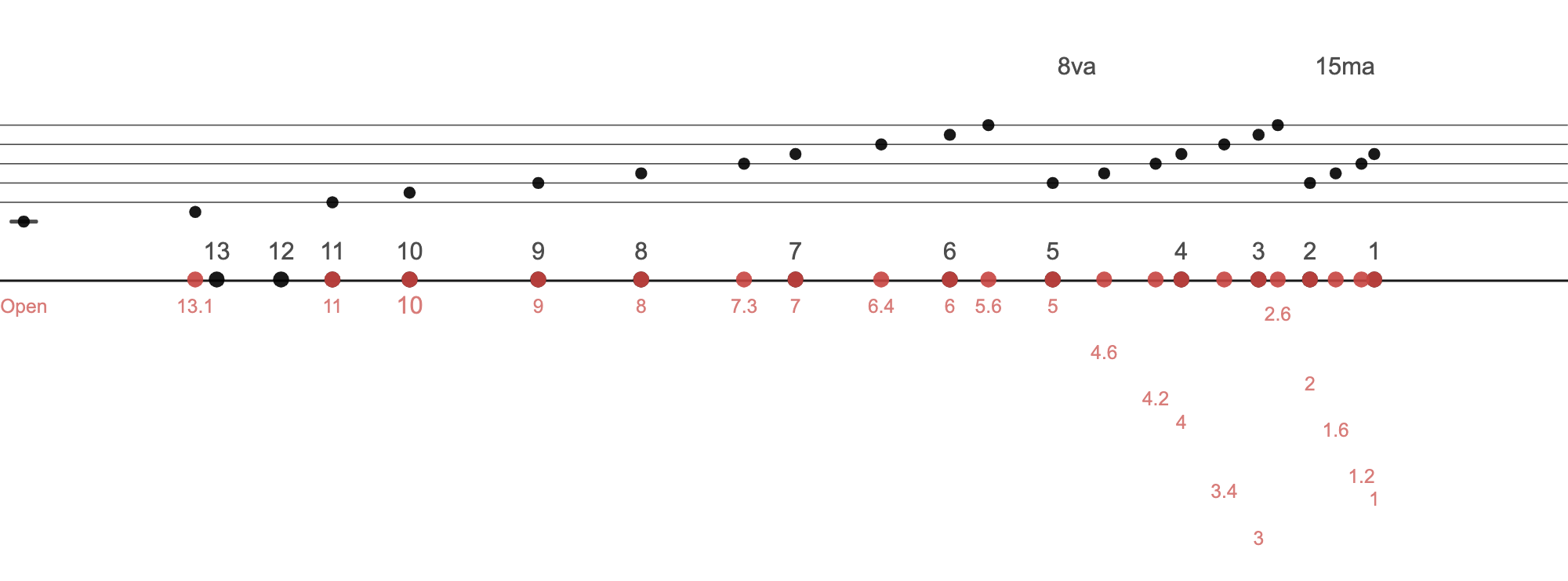
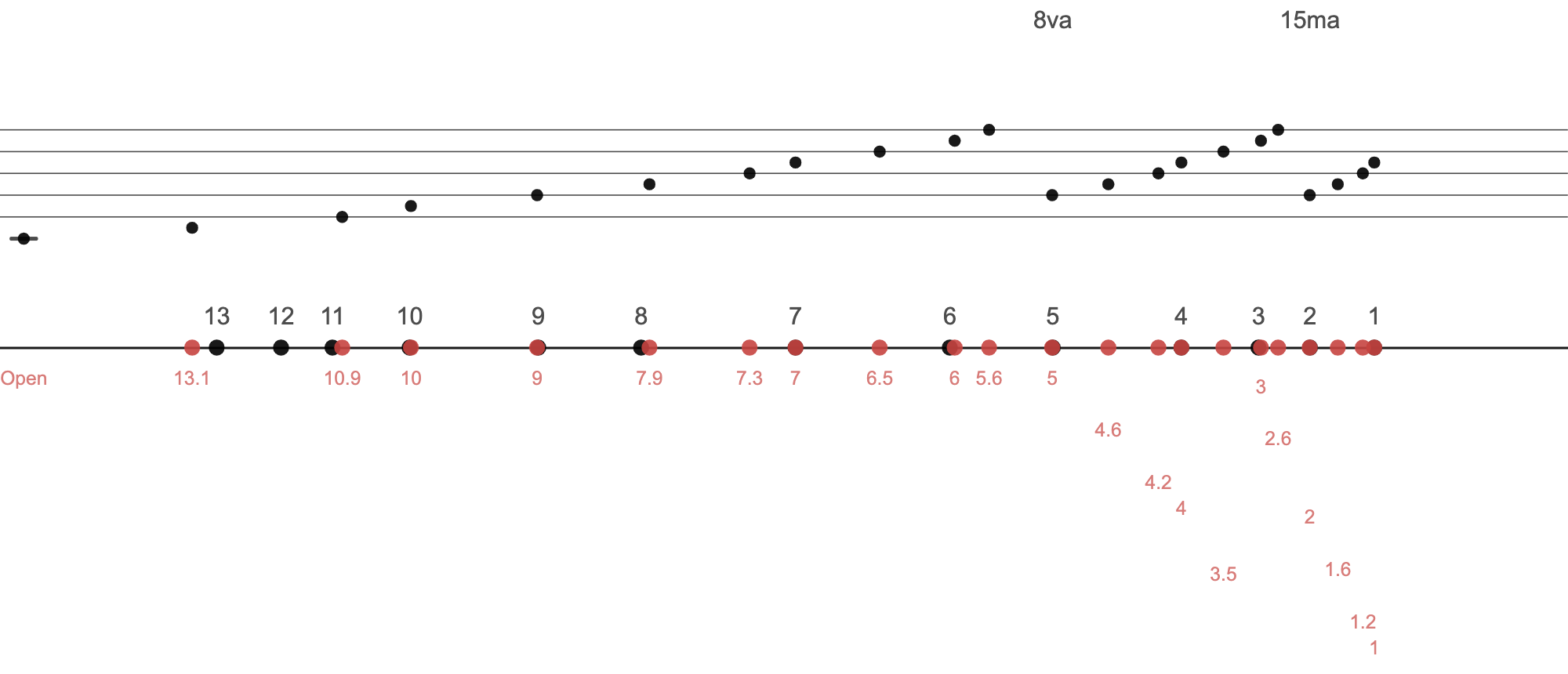
C Major Scale with Equal Temperament Intonation

3.2: Chromatic Scale

And here is the chromatic scale.

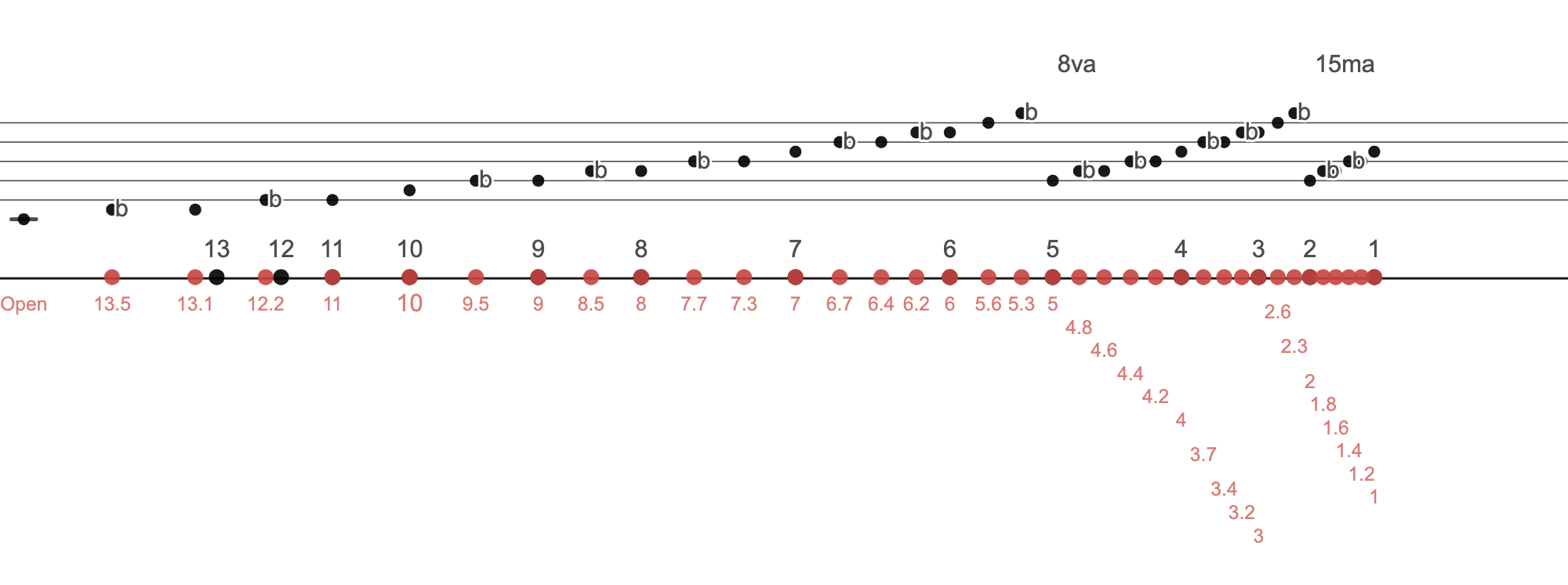
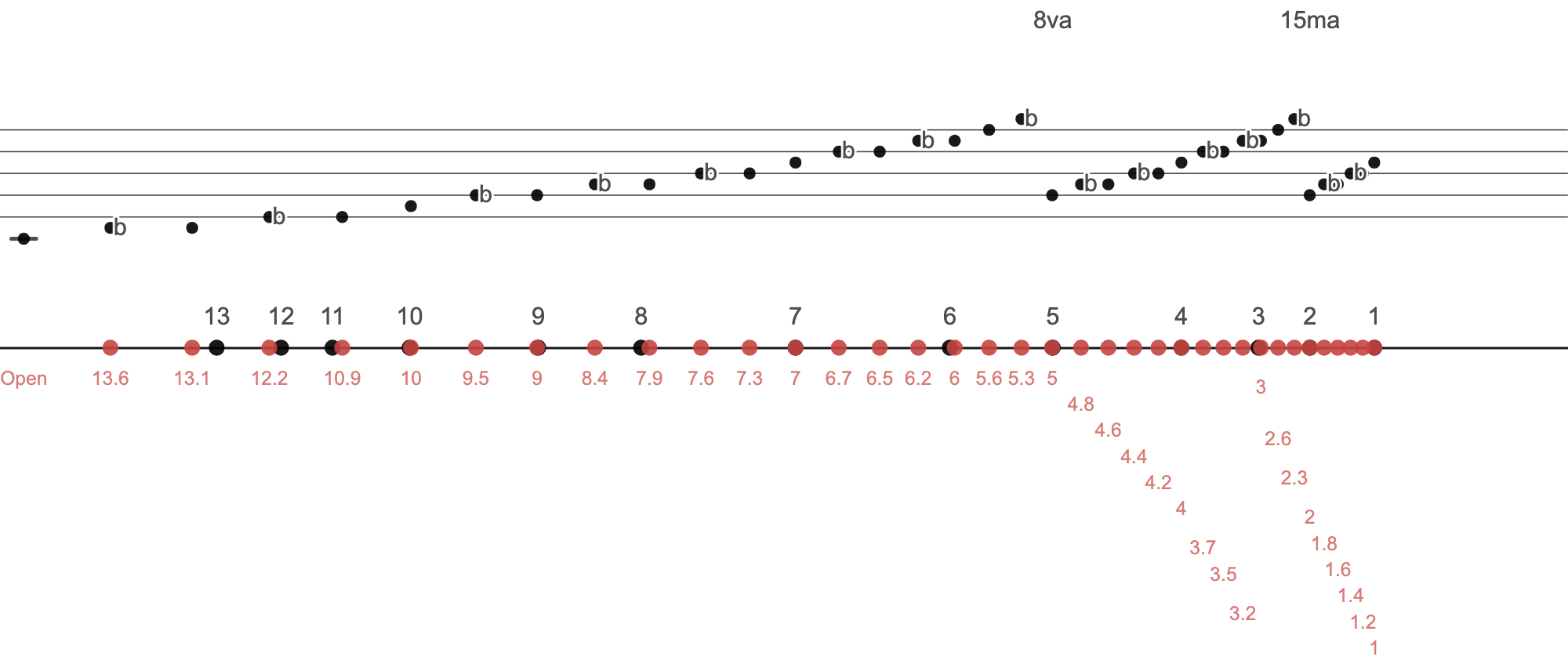
Chromatic Scale with Equal Temperament Intonation

REFERENCE: Desmos page

And here is a handy dandy chart of all these positions mapped to their notes. This follows the standard tuning CDFGACD, though I usually think about this as GACDEGA (same relative pitches).

We can use fancy Excel condition formatting to visualize all the different ways to play a 3: D, for example.

REFERENCE: Note Visualization Excel sheet. Cells in Blue are the ones we can edit to adjust our tuning and note to visualize in green.

For many notes, there are a slew of options for how to plan them. Figuring out the best option is a bit of a logic puzzle. We don't want to jump around too much, so often I try to find a note close by. Above, we can see the same Note (3:D) jumps from the 7th hui to the 3rd hui, covering maybe 10+ inches of playable real estate. Also, the strings do sound different. The higher up, the brighter the sound. If we use a lower hui, the sound is also different (and it's harder to play since the distance between notes are shorter and we need to press down harder).

Ok. Part 1 goes over harmonics (Fàn Yīn 泛音). This post then goes over Sàn Yīn 散音 and Àn Yīn 按音. But how to take this knowledge and put it down on paper when writing or reading music?

To be continued: Part 3: Tablature Old and New